합성곱 - 두 함수 중 반전(reverse), 이동(shift)시켜가며 나머지 함수와의 곱을 연이어 적분하는 것
CNN은 주로 이미지 인식과 음성인식등 다양한 곳에서 사용하는데 특히 이미지 인식에서 기초로 많이 쓰인다.
전체 구조
지금까지 했던 신경망은 인접하는 계층의 모든 뉴런과 결합하여 만드는 완전연결 이엇으며,
이 완전히 연결된 계층을 Affine 계층이라는 이름으로 구현했습니다.
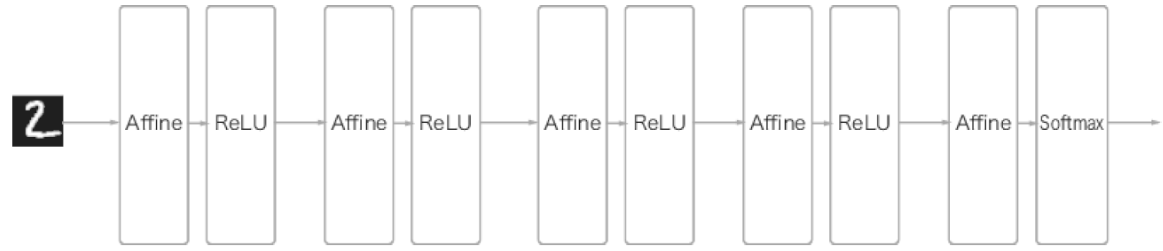
이 완전연결망은 Affine - ReLu 조합이후 마지막에 Affine-Softmax 에서 최종결과를 출력한다.

CNN은 완결연결망에서 '합성곱 계층'과 '풀링 계층'이 추가된다.
즉, 'Conv - ReLU - (Pooling)' 으로 연결된다. (마지막은 Affine - Softmax)
합성곱 계층
각 계층 사이에는 3차원 데이터같이 입체적인 데이터가 흐른다는 점에서 다르다.
완전연결 계층의 문제점 - 데이터의 형상 무시
전에 했던 완전연결 신경망(Affin계층) 은 3차원 데이터를 1차원 데이터로 평탄화 하여 입력을하였다
하지만 실제 이미지인 3차원의 정보를 1차원으로 바꾸면서 가지고 있는 정보를 많이 무시하게 되버린다.
그래서 합성곱은 데이터의 형상을 유지해서 그 문제를 해결한다.
즉, 3차원 데이터로 입력하고 출력한다.
여기서 입출력 데이터를 특징 맵(Feature map) 이라 하고
입력 데이터는 입력 특징 맵(input feature map), 출력데이터를 출력 특징 맵(output feature map)이라는 식이다.
합성곱 연산 (이미지 처리에서 말하는 필터(커널)연산)

합성곱 연산은 필터의 윈도우(회색부분 3X3)를 일정 간격으로 이동해가며 입력 데이터에 적용한다.
회색부분과 필터와의 곱한후 총합을 구한다. 이것을 단일 곱셈 누산(fused multiply-add, FMA)이라 한다.
이것을 출력 장소에 저장하면 된다.

완전 연결 신경망에는 가중치 매개변수와 편향이 존재하지만
CNN에서는 필터의 매개변수가 전에 했던 '가중치'에 해당한다.
그리고 CNN에 편향이 존재하는데 위는 필터 적용까지만 보여주고 다음은 편향을 포함한 과정이다.

패딩
합성곱 연산을 수행하기 전에 입력 데이터 주변을 특정값(ex.0)으로 채우는 것을 패딩(padding)이라고 한다.

위 입력데이터 빈부분에 1을 넣어 출력 크기가 (4,4)가 되게 하였다.
즉, 패딩은 출력 크기를 조정할 목적으로 쓰인다.
스트라이드
필터를 적용하는 위치의 간격을 스트라이드(Stride) 라고한다.

(7,7)은 스트라이드를 적용하기 전은 (5,5) 출력이 나왔으나
스트라이드 2를 적용하니 출력이 (3,3) 출력이 나왔다.
이처럼 출력 크기를 줄일때 스트라이드를 사용한다.
이것을 입력크기(H,W), 필터 크기를(FH, FW), 출력 크기를(OH,OW), 패딩을 P, 스트라이드를 S라 하고 공식을 보면
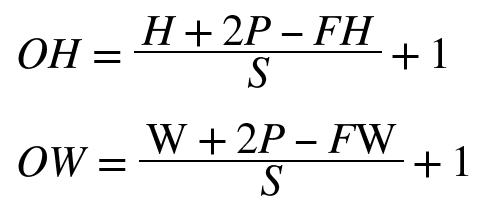
예를 들어 방금 스트라이드를 적용했던 입력: (7,7), 패딩: 0 스트라이드: 2, 필터: (3,3) 이라고 하면
OH = (7 + 2 * 0 - 3) + 1 = 3
OW = (4 + 2 * 0 - 3) + 1 = 3
(3, 3)로 위와 같은 결과가 나왔다.
여기서 정수로 떨어지도록 해야한다.
3차원 데이터의 합성곱 연산
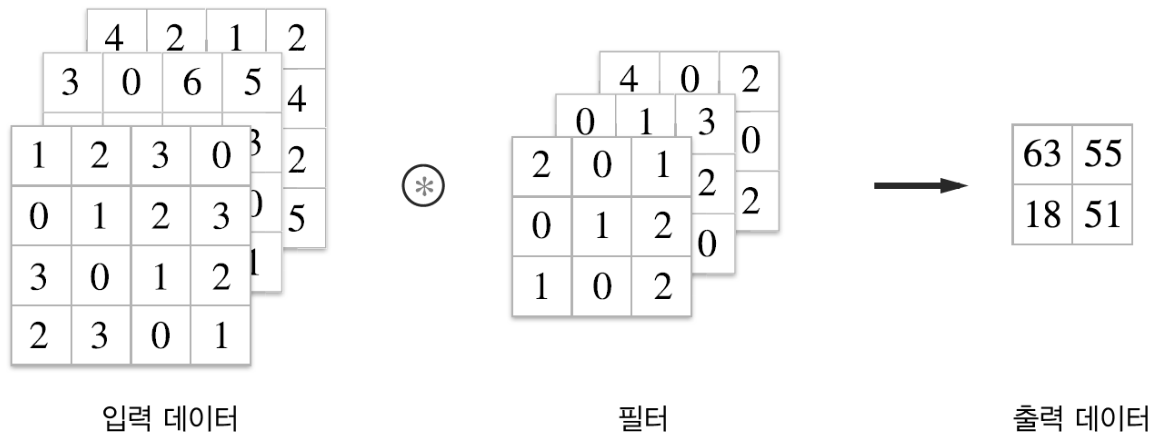

이제 합성곱연산을 블록으로 생각해서 살펴보자

채널이 1인 출력이 나왔다
2이상인 출력이 나오려면 아래와 같이 하면된다.

풀링 계층
스트라이드는 필터를 적용하는 간격을 의미하는데
풀링은 입력데이터중 필터와 연산하는 영역이라고 생각하면 된다.
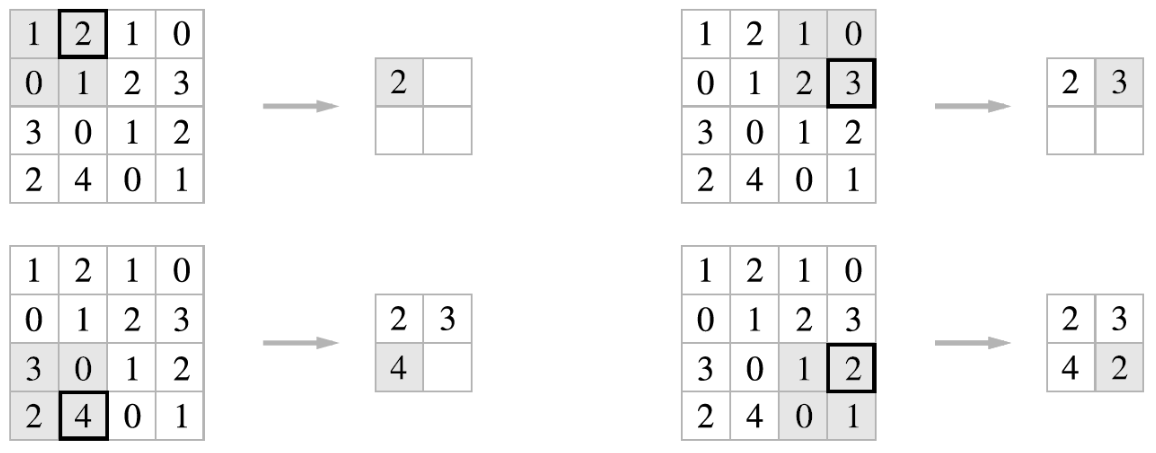
특징
- 학습해야 할 매개변수가 없다.
대상영역에서 최댓값이나 평균을 취하는 명확한 처리이므로 따로 학습할것없이 바로 하면됨
- 채널 수가 변하지 않는다.

- 입력의 변화에 영향을 적게 받는다. (강건하다)
입력 데이터가 조금 변해도 풀링의 결과는 잘 변하지 않는다.

합성곱/풀링 계층 구현하기
합성곱 연산을 그대로 연산하려면 for문을 일일이 써야한다. (풀링마다 필터를 곱해줘야함)
여기서 im2col(image to column)이라는 함수를 사용해서 편하게 해보자~
im2col은 입력데이터를 필터링(가중치 계산) 하기 좋게 전개하는 (펼치는) 함수이다.


위에서는 스트라이드가 곂치지 않았지만 곂치는 경우가 대부분이다.
곂치게 되면 im2col로 전개한 후의 원소 수가 원래 블록의 원소 수보다 많아진다.
그래서 im2col을 사용해 구현하면 메모리를 더 많이 소비하는 단점이 있다.
BUT 컴퓨터는 큰 행렬을 묶어서 계산하는데 탁월하다.
이유는 행렬 계산 라이브러리등은 행렬계산에 고도화로 최적되어 큰 행렬의 곱셈을 빠르게 계산할수 있다.
그래서 행렬 계산으로 만들면 선형 대수 라이브러리를 활용해 효율을 높일수 잇다.
im2col로 입력 데이터를 전개한 다음에는 합성곱 계층의 필터(가중치)를 1열로 전개하고 두 행렬의 곱을 계산해보자

합성곱 계층 구현하기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""다수의 이미지를 입력받아 2차원 배열로 변환한다(평탄화).
Parameters
----------
input_data : 4차원 배열 형태의 입력 데이터(이미지 수, 채널 수, 높이, 너비)
filter_h : 필터의 높이
filter_w : 필터의 너비
stride : 스트라이드
pad : 패딩
Returns
-------
col : 2차원 배열
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
|
cs |
np.pad는 패딩, zeors는 0으로 채우는것
밑에 for문은 최대풀링을 찾는것이다.
다차원에다가 reshape(x,-1)을 하면 다차원의 원소수가 반환된다.
transpose는 다차원 배열의 축 순서를 바꾸는것이다.

그리고 실제 풀링 적용영역을 예시로 들면

전개후 행별 최댓값을 구하고 적절항 형상으로 성형하면 forward처리 끝이다.

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
|
cs |
풀링 계층 구현이다.
풀링 계층 구현은 3단계로 지냏오디는데
- 입력데이터 전개
- 행별 최댓값을 구한다.
- 적절한 모양으로 성형한다.
CNN 구현하기
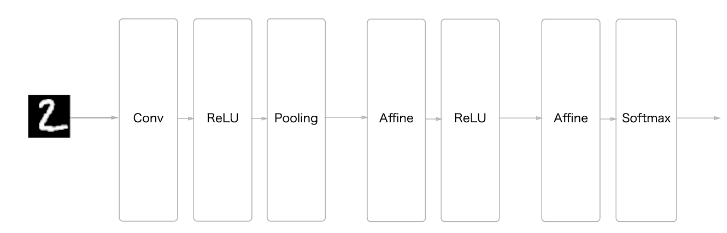
Convolution - ReLU - Pooling - Affine - ReLU - Affine - Softmax
순으로 이뤄진 CNN을 구현해보자
초기화에 인수를 보면
input_dim - 입력데이터(채널 수, 높이,너비)
conv_param - 합성곱 계층의 하이퍼파라미터(딕셔너리), 딕셔너리의 키는 다음과 같다.
- filter_num : 필터수
- filter_size : 필터 크기
- stride : 스트라이드
- pad : 패딩
- hidden_sie : 은닉층(완전연결)의 뉴런수
- output_zie : 출력층(완전연결)의 뉴런수
- weight_init_std : 초기화 때의 가중치 표준편차
초기화 코드 구현
|
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
|
cs |
초기화 인수로 주어진 합성곱 계층의 하이퍼파라미터를딕셔너리에서 꺼낸다.
|
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
|
cs |
위 초기화 함수뒤에 붙는것으로 학습에 필요한 매개변수인 1번째 층의 합섭곱 계층과 나머지 두 완전 연결계층의 가중와 편향을 인스턴스 변수 params 딕셔너리에 저장한다. 1번째 층의 합성곱 계층의 가중치를 W1, 편향을 b1으로 저장한다.(2번,3번도 마찬가지)
|
# 계층 생성
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
|
cs |
이것도 초기화 함수 뒤에 붙는것으로
순서가 있는 딕셔너리인 layer에 계층을 차례로 추가한다.
SoftmaxWithLoss 계층만큼은 last_layer라는 별도 변수에 저장한다.
|
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""손실 함수를 구한다.
Parameters
----------
x : 입력 데이터
t : 정답 레이블
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
|
cs |
predict 메서드는 초기화 때 layers에 추가된 계층을 맨 앞에서부터 차례로 forward 메서드를 호출하며 그결과를 다음층에 전달한다. loss 메서드는 predict 메서드의 결과를 인수로 마지막 층의 forward 메서드를 호출하여 첫계층부터 마지막 계층까지 forward를 처리한다.
|
def gradient(self, x, t):
"""기울기를 구한다(오차역전파법).
Parameters
----------
x : 입력 데이터
t : 정답 레이블
Returns
-------
각 층의 기울기를 담은 사전(dictionary) 변수
grads['W1']、grads['W2']、... 각 층의 가중치
grads['b1']、grads['b2']、... 각 층의 편향
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
|
cs |
오차역전법으로 기울기를 구현한 것이다.
이과정은 순전파와 역전파를 반복하는 것인데 위는 그 함수들을 호출한것이다
이제 이 SimpleConvNet으로 MNIST 데이터셋을 학습해볼 것이다.

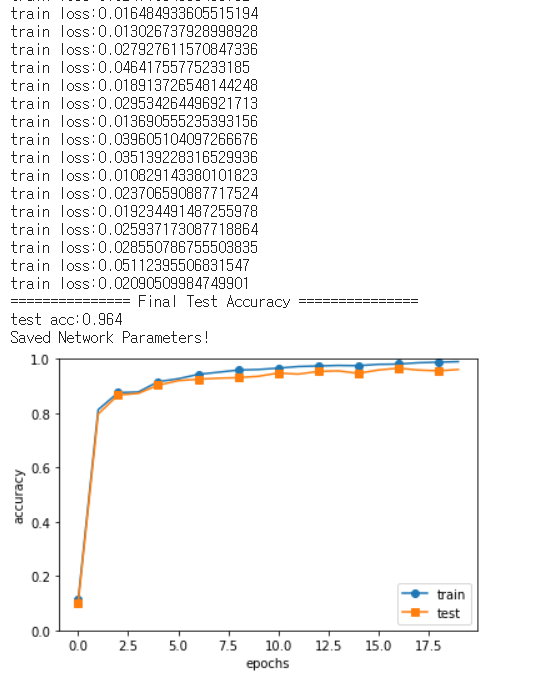
데이터셋을 모두 하면 시간이 너무 오래걸려서 train 5000, test1000으로 제한해서 실행했다.
모든 데이터를 하면 시험데이터에 대한 정확도가 99%에 이른다.
이처럼 합성곱 계층과 풀링 계층은 이미지 인식에 필수적인 모듈이다.
CNN 시각화하기
이번에는 합성곱 계층을 시각화해서 CNN이 보고 있는 것이 무엇인지 알아보자
1번째 층의 가중치 시각화
앞에서 MINIST 데이터셋으로 CNN 학습을 해보았는데
그때 1번째 층의 합성곱 계층의 가중치는 그 형상이 (30, 1, 5, 5)이다.
- 필터크기 5X5, 채널1개라는것은 이필터를 1채널의 회색조 이미지로 시각화 힐수 있다는것이다.(회색조?)
합성곱 계층(1층째) 필터를 이미지로 나타내 보자

학습 전 필터는 무작위로 초기화 되어 있었는데 학습후 어느정도 규칙성이 있어졌다.
그럼 규칙성 있는 필터는 '무엇을 보고 있는' 걸까?
그것은 에지(색상이 바뀐 경계선)와 블롭(국소적으로 덩어리진 영역) 등을 보고 있다.
예를들어 왼쪽 절반이 흰색이고 오른쪽 절반이 검은색인 필터는 아래와 같이 세로방향의 에지에 반응하는 필터이다.
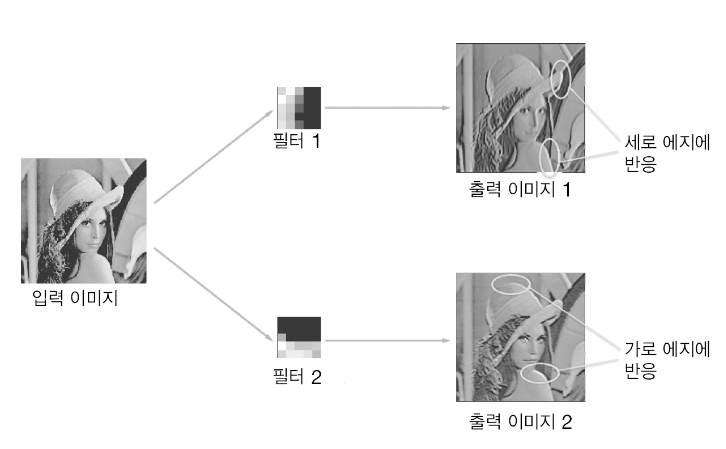
이처럼 합성곱 계층의 필터는 에지나 블롭 등의 원시적인 정보를 추출할 수 있다.
원시적인 정보가 뒷단 계층에 전달된다는 것이 앞에서 구현한 CNN에서 일어나는 일이다.
층깊이에 따른 추출 정보 변화
앞의 1번째 층 합성곱계층에서는 에지나 블롭등 저수준의 정보가 추출된다.
그럼 곂곂이 쌓인 CNN의 각 계층에서는 어떤 정보가 추출되는지 알아보면
계층이 깊어질수록 추출되는 정보는 더 추상화 된다는 것을 알 수 있다.

위 구조는 합성곱 계층과 풀링 계층을 여러 겹 쌓고, 마지막으로 완전 연결 계층을 거쳐 결과를 출력하는 구조이다.
블록으로 나타낸것은 중간데이터이며, 그 중간 데이터에 합성곱 연산을 연속해서 적용한다.
층이 깊어지면서 고급정보로 변화해간다.
대표적인 CNN
LeNet
손글씨 숫자를 인식하는 네트워크

위와 같이 합성곱 계층과 풀링 계층(단순히 '원소를 줄이기'만 하는 서브 샘플링 계층)을 반복하고
마지막으로 완전연결 계층을 거치면서 결고를 출력한다.
LeNet과 '현재의 CNN'을 비교하면 차이가 있는데,
첫번째는 활성화 함수이다. LeNet은 시그모이드 함수를 사용하는데, 현재는 주로 ReLU를 사용한다
두번째는 원래의 LeNet은 서브샘플링을 하여 중간 데이터의 크기를 줄이지만 현재는 최대 풀링이 주류이다.
이처럼 처음 제안된 CNN인 LeNet과 차이가 별로 안난다.
AlexNet
2012년에 발표된 AlexNet은 딥러닝 열풍을 일으키는 큰 역할을 했다고한다.

보면 LeNet과 차이가 별로 없다.
AlexNet은 합성곱 계층과 풀링 계층을 거듭하여 마지막으로 완전 연결 계층을 거쳐 결과를 출력한다.
LeNet과 다른점은
- 활성화 함수로 ReLU를 사용
- LRN(Local Response Normalization)이라는 국소적 정규화를 실시하는 계층을 이용한다.
- 드롭아웃을 실행한다.
별차이는 없지만 주변환경과 컴퓨터 기술이 크게 성장하여 대량의 데이터를 누구나 얻게 되었고,
병렬계산에 특화된 GPU가 보급되면서 대량의 연산을 고속으로 수행할 수 있게 되었다.
빅데이터, GPU, 이것이 딥러닝 발전의 원동력이라고한다.
'DATA Science > DeepLearing from scratch' 카테고리의 다른 글
| 딥러닝 (0) | 2021.05.23 |
|---|---|
| 딥러닝 학습 관련 기술들 (0) | 2021.05.17 |
| 오차역전파법 (0) | 2021.05.14 |
| 신경망 학습 - 학습 알고리즘 구현 (0) | 2021.05.13 |
| 신경망 학습 (2) | 2021.05.12 |




댓글