수치미분을 통하여 신경망의 가중치 매개변수를 구했지만 수치미분은 시간이 오래걸린다.
계산그래프
계산 그래프를 통하여 계산과정을 알아보면 오차역전파법을 잘 이해할수 있다.

위처럼 어떠한 값을 수식에 넣고 계산해 나가는 것이 계산그래프 같은것.
문제의 흐름을 살펴 보면 1. 계산 그래프를 구성 2. 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다.
이처럼 왼쪽에서 오른쪽으로 진행하는 단계를 순전파(forward propagation)라고 한다.
이것을 반대로 한다면 역전파(backward propagation) 라고 한다.
계산그래프를 사용하는 목적은 국소적계산과 역전파를 통해 '미분'을 효율적으로 계산할 수 있는 점에 있다.
국소적계산 - 각 노드에서 단순한 계산을 하고 중간에 저장을 할수 있다.

역전파를 사용하면 미분값을 전달하여 값을 구할수가 있다.
연쇄법칙
위 국소적 미분을 전달하는 원리는 연쇄법칙이다.

계산절차를 보면 신호 E에 노드의 국소적 미분을 곱한 후 다음 노드로 전달한다.
여기서 국소적 미분은 순전파때의 미분을 구한다는것이고 x에 대한 y의 미분을 구하는것이다.
합성함수 : 여러 함수로 구성된 함수
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
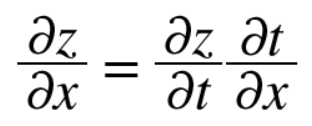

위 식을 연쇄법칙을 통해 미분δz/δx를 구해보면




역전파
이처럼 연쇄법칙은 이뤄 진다는 것을 알수 있었다.
이제 역전파의 구조를 설명해보자
- 덧셈노드의 역전파
z=x+y를 대상으로 역전파를 살펴보자
미분은dz/dx =1, dz/dy =1 이 될것이다.


- 곱셈노드의 역전파
z=xy라고 가정하면
미분값은 dz/dx=y, dz/dy=x 이다

덧셈 노드 역전파와 달리 곱셈 노드 역전파의 경우 그대로 값을 보내지 않아서 순방향입력신호가 필요하여 곱셈노드 역전파 구현시 순전파의 입력 신호를 변수에 저장해둡니다.
단순한 계층 구현
위에서 해던것을 파이썬으로 구현한다. 곱셉노드를 mulLayer, 덧셈노드를 addLayer
곱셈계층
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # x와 y를 바꾼다.
dy = dout * self.x
return dx, dy
|
cs |
여기서 dout은 미분값


덧셈계층
덧셈계층은 곱셈계층과 구성은 같으나 그대로 보내주는것이므로 역전파쪽만 바꿔주면되므로 그냥 적겟다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
|
cs |
이제 덧셈 계층과 곱셈 계층을 사용하여 사과2개, 귤2개를 사는 상황을 구현하자
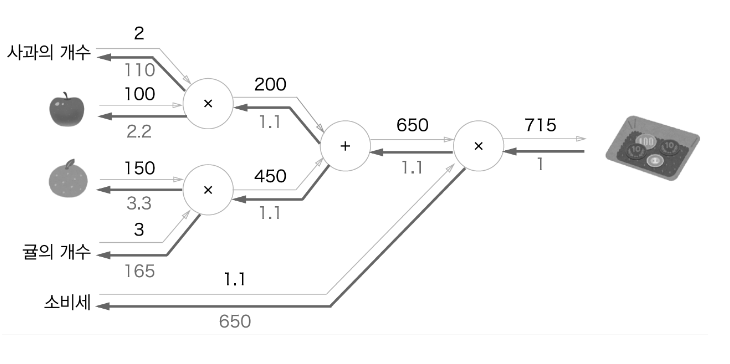

활성화 함수 계층 구현하기
이제 계산 그래프를 신경망에 적용해보자.
신경망을 구성하는 층 각각을 클래스 하나로 구현한다.
ReLU와 Sigmoid 계층을 구현하겠다.
ReLU 계층
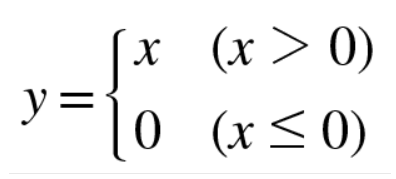

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Relu:
def __init__(self) -> None:
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
|
cs |
Relu 클래스를 코드화 하면 이와 같다.
여기서 mask라는 것이 나오는데 True/false로 구성된 넘파이 배열이다.
Sigmoid 계층
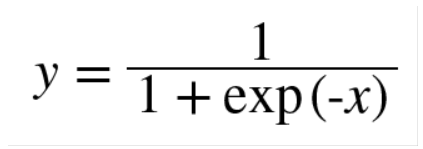
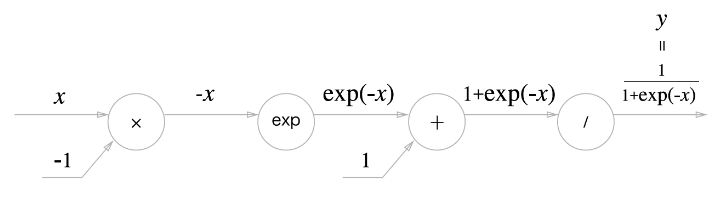
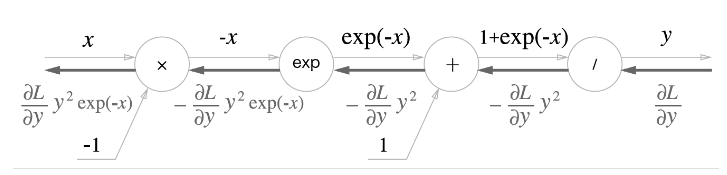
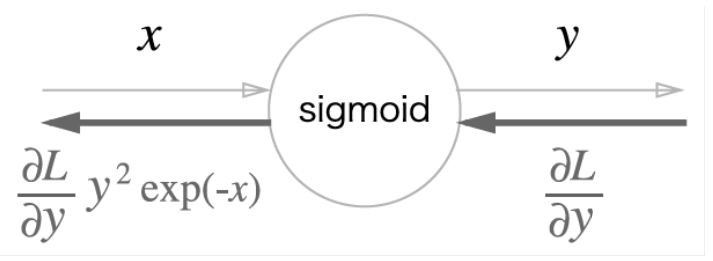
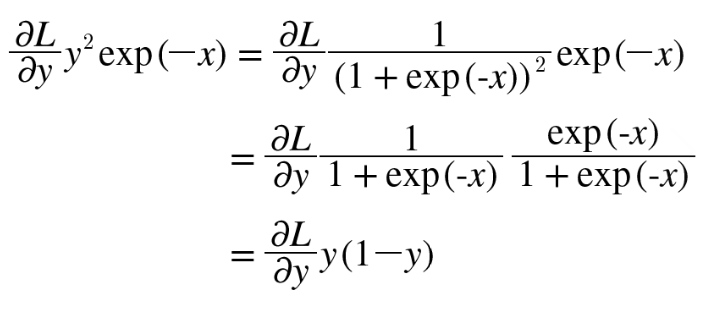
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Sigmoid:
def __init__(self) -> None:
self.mask = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
|
cs |
코드화
Affine/Softmax 계층구현하기
어파인 변환(Affine transformation) : 신경망의 순전파 때 수행하는 행렬의 곱
어파인 변환을 수행하는 처리를 'affine 계층'이라 함
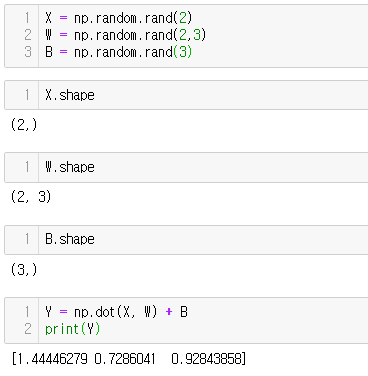
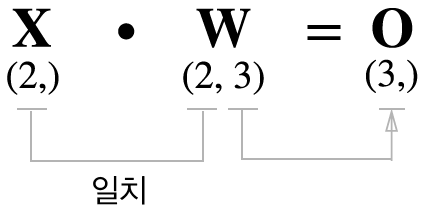
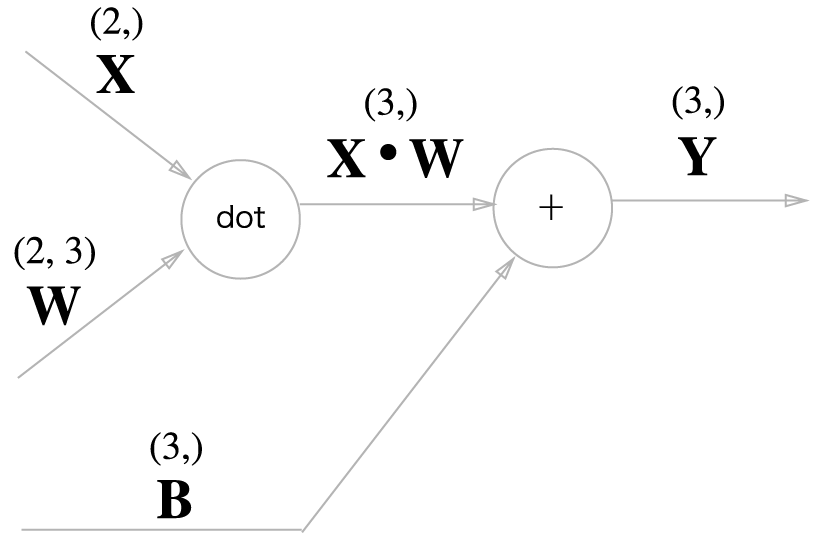
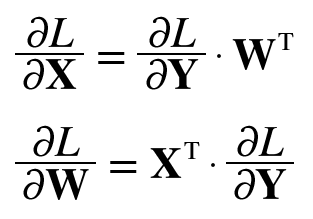
WT는 전치 행렬을 뜻한다.
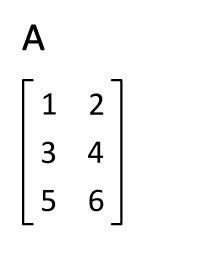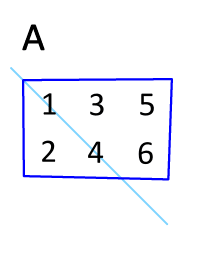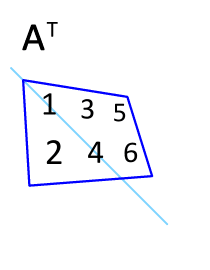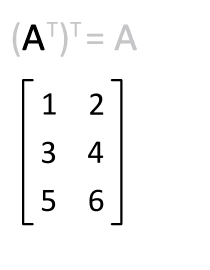
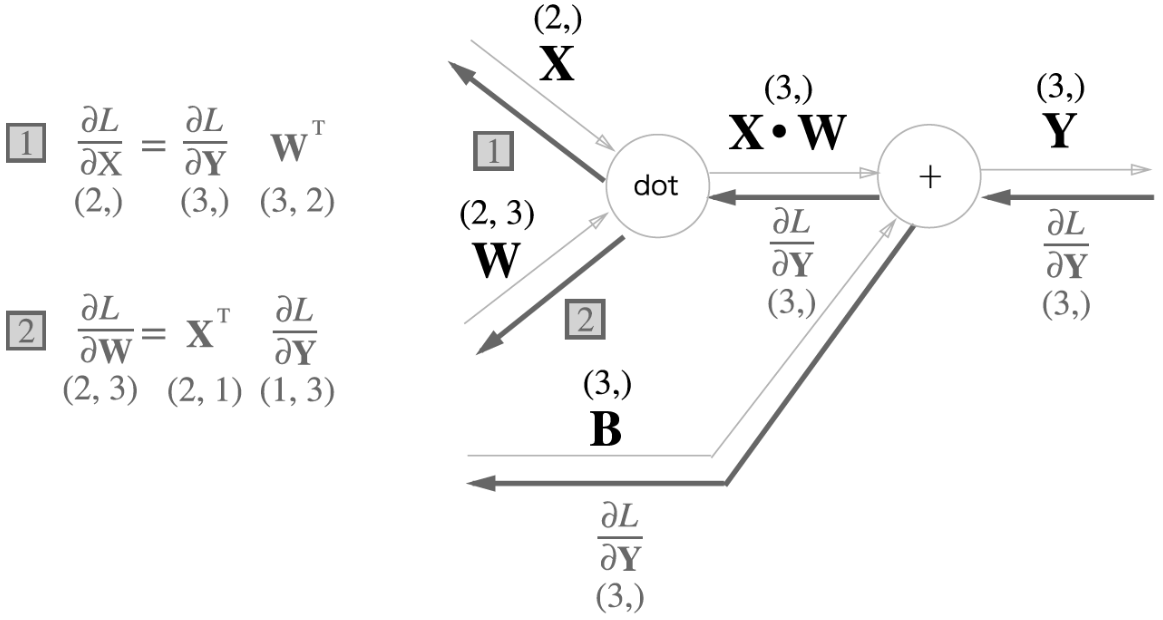
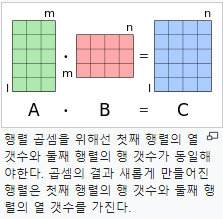
위 그림에서 주의 해야할것은 형상. 즉 행렬의 차원 원소수를 조심해야한다.
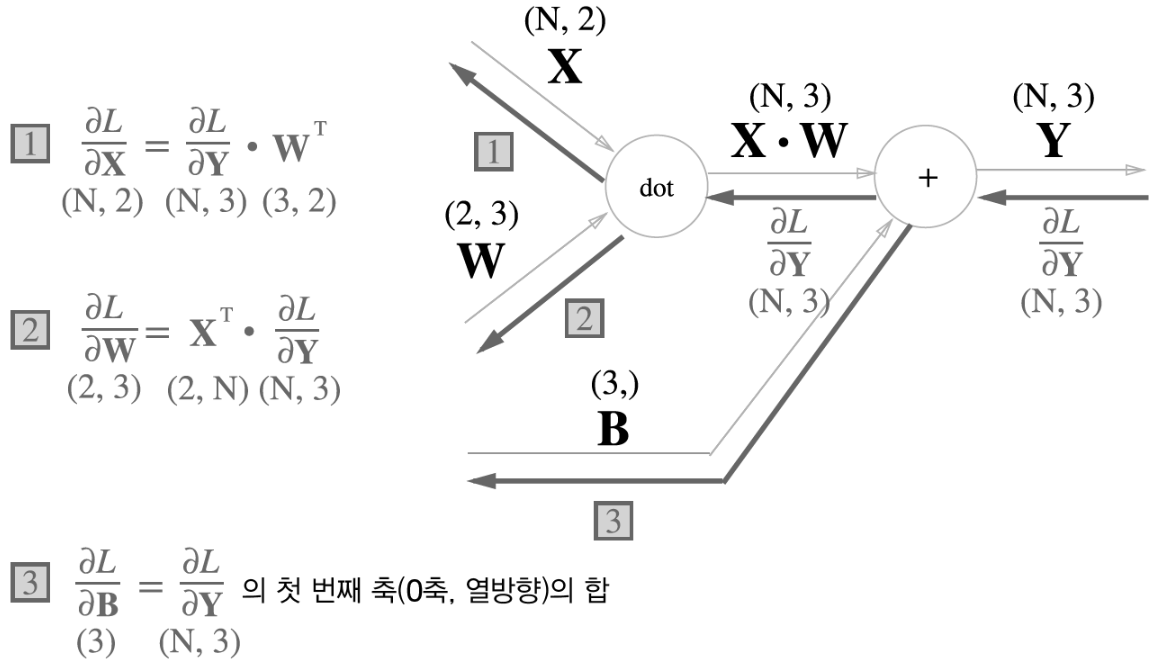
배치용 Affine 계층
지금까지는 입력데이터로 X를 하나(스칼라값)을 입력햇다.
이번에는 데이터를 N개 넣어 X를 (N,2)로 입력해보자.
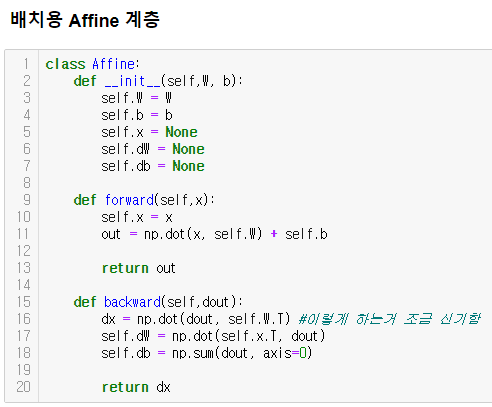
Softmax-with-Loss 계층
출력층에서 사용하는 소프트맥스 함수에 대해 살펴 보면 입력값을 정규화하여 출력한다.
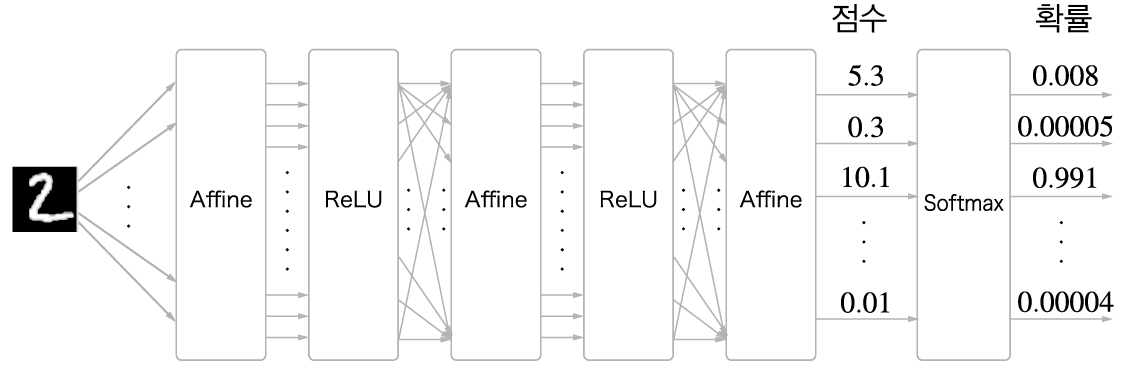
여기서 Softmax 계층 입력값을 정규화(출력의 합이 1이 되도록)하여 출력하고,
입력은 숫자가 10가지 이므로 10개이다.
신경망에서 수행하는 작업은 학습과 추론.
추론할때는 일반적으로 Softmax 계층은 사용하지 않는다. (위처럼 Affine계층의 출력을 인식결과로 사용한다.)
신경망에서 정규화하지 않은 출력 결과를 점수(score)라고 한다.
즉, 신경망 추론에서 답을 하나만 내는경우에는 가장 높은 점수만 알면 되니 Softmax 계층은 필요 없다.
But 신경망 학습에서는 Softmax 계층은 필요하다.
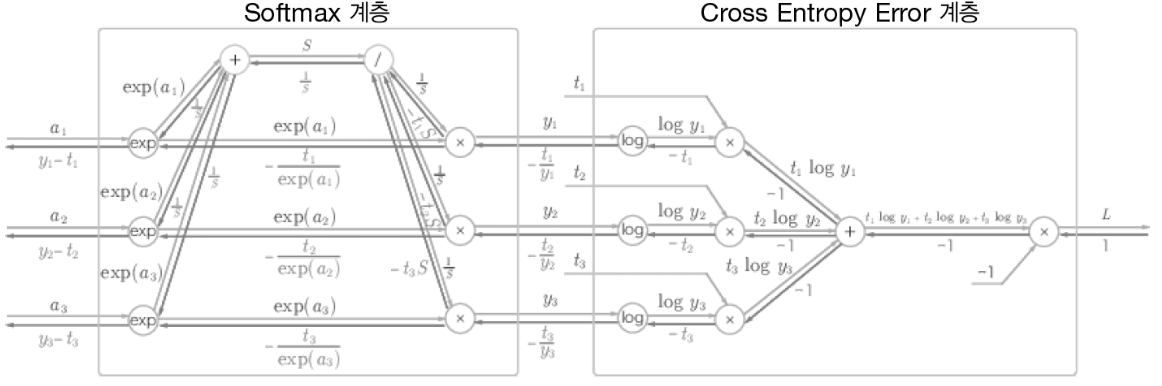
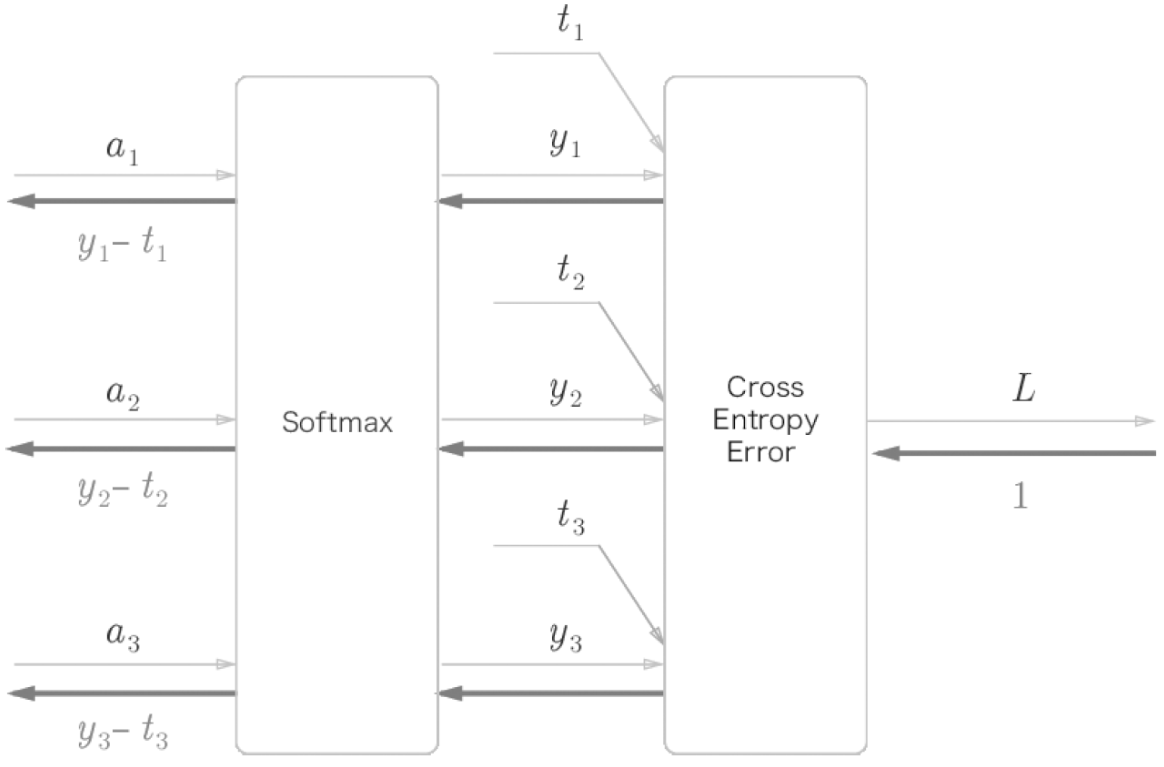
여기서 결과가 (y1-t1, y2-t2, y3-t3)이라는 점에 주목해야한다.
(y1,y2,y3)는 Softmax 계층의 출력, (t1,t2,t3)는 정답레이블이므로
위 결과가 Softmax계층의 출력과 정답레이블의 차분인것이다.
이 차이인 오차가 앞 계층에 전해지는 것이다.
신경망 학습의 목적은
신경망 출력(Softmax의 출력)이 정답 레이블과 가까워지도록 가중치 매개변수의 값을 조정하는 것이다.
그래서 오차를 효율적으로 앞 계층에 전달해야한다.

오차역전파법 구현하기
전제
신경망에는 적응 가능한 가중치와 편향이 있고,
이 가중치와편향을 훈련데이터에 적응하도록 저정하는 과정이 학습이다.
신경망 학습은 4단계로 수행한다.
1단계 - 미니배치
훈련 데이터 중 일부를 무작위로 가져온다. 이렇게 선별한 데이터를 미니배치라 하며,
이 미니배치의 손실 함수 값을 줄이는 것이 목표이다.
2단계 - 기울기 산출
미니 배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구하는것.
3단계 - 매개변수 갱신
가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
4단계 - 반복
1~3단계를 반복한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
|
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
|
cs |
layers: 순서가 있는 딕셔너리 변수로 신경망의 계층 보관
lastLayer: 신경망의 마지막 계층으로, SoftmaxWithLoss 계층
오차역전파법으로 구한 기울기 검증하기
수치 미분은 구현하기 쉽지만 버그가 별로 없으나 오차역전법은 구현하기 복잡하여 오류가 많으므로
서로 비교하여 일치하는 작업인 기울기 확인(gradient check)을 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]
grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)
# 각 가중치의 절대 오차의 평균을 구한다.
for key in grad_numerical.keys():
diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )
print(key + ":" + str(diff))
|
cs |
오차역전파법을 사용한 학습구현하기
다른점은 기울기를 오차역전파법이라는것 빼고는 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
#grad = network.numerical_gradient(x_batch, t_batch) # 수치 미분 방식
grad = network.gradient(x_batch, t_batch) # 오차역전파법 방식(훨씬 빠르다)
# 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)
|
cs |
'DATA Science > DeepLearing from scratch' 카테고리의 다른 글
| CNN --- 합성곱 신경망 (0) | 2021.05.20 |
|---|---|
| 딥러닝 학습 관련 기술들 (0) | 2021.05.17 |
| 신경망 학습 - 학습 알고리즘 구현 (0) | 2021.05.13 |
| 신경망 학습 (2) | 2021.05.12 |
| 신경망 (0) | 2021.05.12 |




댓글